الكمية التي تميز توزيع الطاقة على طيف الإشارة وتسمى الكثافة الطيفية للطاقة موجودة فقط للإشارات التي تكون فيها الطاقة خلال فترة زمنية لا نهائية محدودة، وبالتالي، ينطبق تحويل فورييه عليها.

بالنسبة للإشارات التي لا تضمحل بمرور الوقت، تكون الطاقة كبيرة بشكل لا نهائي وتتباعد بشكل متكامل (1.54). ضبط طيف السعة غير ممكن. ومع ذلك، فإن متوسط ​​الطاقة Рсп، تحدده العلاقة

تبين أنها محدودة. ولذلك، يُستخدم المفهوم الأوسع المتمثل في "الكثافة الطيفية للقدرة". دعونا نعرّفها على أنها مشتق متوسط ​​قدرة الإشارة فيما يتعلق بالتردد ونشير إليها بالرمز Сk(п):

يؤكد الفهرس k أننا هنا نعتبر الكثافة الطيفية للقدرة خاصية للدالة الحتمية u(t) التي تصف تنفيذ الإشارة.

تعتبر خاصية الإشارة هذه أقل أهمية من الكثافة الطيفية للسعة، لأنها خالية من معلومات الطور [انظر. (1.38)]. لذلك، من المستحيل إعادة بناء تنفيذ الإشارة الأصلية منه بشكل لا لبس فيه. ومع ذلك، فإن غياب معلومات الطور يسمح لنا بتطبيق هذا المفهوم على الإشارات التي لم يتم تعريف الطور لها.

لإنشاء اتصال بين الكثافة الطيفية Сk(x) وطيف الاتساع، سنستخدم الإشارة u(t) الموجودة خلال فترة زمنية محدودة (-T<. t

أين هي الكثافة الطيفية للقدرة لإشارة محدودة الوقت.

وسيظهر لاحقاً (انظر الفقرة 11.1) أنه من خلال حساب متوسط ​​هذه الخاصية على العديد من الإنجازات، من الممكن الحصول على الكثافة الطيفية للقدرة لفئة كبيرة من العمليات العشوائية.

وظيفة الارتباط التلقائي للإشارة الحتمية

يوجد الآن خاصيتان في مجال التردد: الاستجابة الطيفية والكثافة الطيفية للقدرة. الخاصية الطيفية، التي تحتوي على معلومات كاملة عن الإشارة u(t)، تتوافق مع تحويل فورييه في شكل دالة زمنية. دعونا نتعرف على ما تتوافق معه الكثافة الطيفية للقدرة، الخالية من معلومات الطور، في المجال الزمني.

ينبغي افتراض أن نفس الكثافة الطيفية للقدرة تقابل العديد من الوظائف الزمنية التي تختلف في الطور. العالم السوفيتي L.Ya. اكتشف خينشين والعالم الأمريكي ن. وينر في وقت واحد تقريبًا تحويل فورييه العكسي لكثافة القدرة الطيفية:

دعونا نسمي دالة الوقت المعممة r()، التي لا تحتوي على معلومات المرحلة، وظيفة الارتباط الذاتي للوقت. ويبين درجة الارتباط بين قيم الدالة u(t) مفصولة بفاصل زمني، ويمكن استخلاصها من النظرية الإحصائية من خلال تطوير مفهوم معامل الارتباط. لاحظ أنه في دالة الارتباط الزمني، يتم تنفيذ المتوسط ​​بمرور الوقت ضمن إدراك واحد لمدة طويلة بما فيه الكفاية.

العلاقة التكاملية الثانية لزوج تحويل فورييه صالحة أيضًا:

مثال 1.6 تحديد وظيفة الارتباط الذاتي الزمني للإشارة التوافقية u(t) = u0 cos(t-ts). وفقا ل(1.64)

تنفيذ التحولات البسيطة

أخيرا لدينا

كما هو متوقع، ru() لا يعتمد على μ، وبالتالي، (1.66) صالح لمجموعة كاملة من التوافقيات التي تختلف في المراحل.

المؤسسة التعليمية الدولية

كلية العلوم التطبيقية

مقال

حول هذا الموضوع"طيف كثافة القدرة وعلاقته بوظيفة الارتباط"

بالانضباط"نظرية الاتصالات الكهربائية »

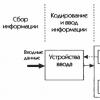
إجراء:طالب المجموعة

فبن-ريت(ض)-4S *

جوماجلدين د

التحقق:جلوخوفا إن.في.

ألماتي، 2015

I. مقدمة

الجزء الثاني الرئيسي

1. الكثافة الطيفية للطاقة

1.1 المتغيرات العشوائية

1.2 الكثافة الاحتمالية لدالة المتغير العشوائي

2. عملية عشوائية

3. طريقة تحديد الكثافة الطيفية للقدرة باستخدام دالة الارتباط

ثالثا الاستنتاج

IV قائمة الأدبيات المستخدمة

مقدمة

تنظر نظرية الاحتمالية إلى المتغيرات العشوائية وخصائصها في "الإحصائيات". إن مشكلة وصف ودراسة الإشارات العشوائية “في الديناميكيات”، باعتبارها انعكاسا للظواهر العشوائية التي تتطور مع مرور الوقت أو وفقا لأي متغير آخر، يتم حلها من خلال نظرية العمليات العشوائية.

كقاعدة عامة، سوف نستخدم المتغير "t" كإحداثي عام لتوزيع المتغيرات العشوائية على متغير مستقل ونتعامل معه، من أجل الملاءمة فقط، كإحداثي زمني. عادةً ما تسمى توزيعات المتغيرات العشوائية في الوقت، وكذلك الإشارات التي تعرضها بأي شكل رياضي، بالعمليات العشوائية. في الأدبيات التقنية، يتم استخدام مصطلحي "إشارة عشوائية" و"عملية عشوائية" بالتبادل.

في عملية معالجة وتحليل البيانات المادية والتقنية، يتعين على المرء عادة التعامل مع ثلاثة أنواع من الإشارات الموصوفة بالطرق الإحصائية. أولاً، هذه إشارات معلومات تعكس العمليات الفيزيائية ذات الطبيعة الاحتمالية، مثل، على سبيل المثال، أعمال تسجيل جزيئات الإشعاع المؤين أثناء تحلل النويدات المشعة. ثانيًا، إشارات المعلومات التي تعتمد على معلمات معينة للعمليات أو الأشياء الفيزيائية، والتي تكون قيمها غير معروفة مسبقًا، والتي يمكن عادةً تحديدها من إشارات المعلومات هذه. وثالثًا، هذا هو الضجيج والتداخل، المتغير بشكل عشوائي مع مرور الوقت، والذي يصاحب إشارات المعلومات، ولكنه كقاعدة عامة، مستقل إحصائيًا عنها سواء في قيمها أو في التغييرات بمرور الوقت.

الكثافة الطيفية للطاقة

تسمح الكثافة الطيفية للقدرة للمرء بالحكم على خصائص التردد لعملية عشوائية. وهو يميز شدتها عند ترددات مختلفة أو، بمعنى آخر، متوسط ​​الطاقة لكل وحدة تردد.

يسمى توزيع متوسط ​​الطاقة عبر الترددات بطيف الطاقة. يسمى الجهاز الذي يقيس طيف الطاقة بمحلل الطيف. يُطلق على الطيف الموجود نتيجة للقياسات اسم طيف الأجهزة.

يعمل محلل الطيف على أساس طرق القياس التالية:

· طريقة التصفية.

· طريقة التحويل طبقاً لنظرية فينر-هنشن.

· طريقة تحويل فورييه.

· طريقة استخدام وظائف الإشارة.

· طريقة تطبيق الأجهزة للوظائف المتعامدة.

خصوصية قياس طيف الطاقة هي المدة الكبيرة للتجربة. وفي كثير من الأحيان يتجاوز مدة وجود التنفيذ، أو الوقت الذي يبقى خلاله سكون العملية قيد الدراسة. إن تقديرات طيف القدرة التي يتم الحصول عليها من تطبيق واحد لعملية إرجودية ثابتة ليست مقبولة دائمًا. في كثير من الأحيان يكون من الضروري إجراء قياسات عديدة، لأنه من الضروري حساب متوسط ​​الإنجازات مع مرور الوقت وعلى المجموعة. في كثير من الحالات، يتم حفظ تطبيقات العمليات العشوائية قيد الدراسة مسبقًا، مما يجعل من الممكن تكرار التجربة عدة مرات مع تغيير مدة التحليل، باستخدام خوارزميات ومعدات معالجة مختلفة.

في حالة التسجيل الأولي لتطبيقات عملية عشوائية، يمكن تقليل أخطاء الأجهزة إلى قيم بسبب مدة التنفيذ المحدودة وعدم الثبات.

يتيح لك حفظ التطبيقات التي تم تحليلها تسريع تحليل الأجهزة وأتمتته.

المتغيرات العشوائية

يتم وصف المتغير العشوائي بالقوانين الاحتمالية. احتمال أن تكون كمية مستمرة Xعند قياسها سوف تقع في أي فترة زمنية × 1<х <х 2 ، يتم تحديده بالتعبير:

، أين ع (خ)- كثافة الاحتمال، و. للمتغير العشوائي المنفصل x i P(x = x i)=P i، أين باي- الاحتمال المقابل للمستوى الأول للكمية X.

عند دراسة أنظمة التحكم الآلي، من المناسب استخدام خاصية أخرى للعملية العشوائية الثابتة، تسمى الكثافة الطيفية. في كثير من الحالات، خاصة عند دراسة تحويل العمليات العشوائية الثابتة بواسطة أنظمة التحكم الخطية، تبين أن الكثافة الطيفية هي خاصية أكثر ملاءمة من دالة الارتباط. يتم تعريف الكثافة الطيفية لعملية عشوائية على أنها تحويل فورييه لوظيفة الارتباط، أي.

إذا استخدمنا صيغة أويلر، فيمكن تمثيل (9.52) على النحو التالي

وبما أن الدالة فردية، فإن التكامل الثاني في التعبير الأخير يساوي صفرًا. مع الأخذ بعين الاعتبار أن الدالة زوجية، نحصل على

لأنه يتبع من (9.53) ذلك

وبالتالي، فإن الكثافة الطيفية هي دالة حقيقية وحتى للتردد o). لذلك، على الرسم البياني، تكون الكثافة الطيفية دائمًا متناظرة حول المحور الإحداثي.

إذا كانت الكثافة الطيفية معروفة، فباستخدام صيغة تحويل فورييه العكسية، يمكنك العثور على دالة الارتباط المقابلة:

وباستخدام (9.55) و(9.38) يمكننا إنشاء علاقة مهمة بين التشتت والكثافة الطيفية لعملية عشوائية:

يرجع أصل مصطلح "الكثافة الطيفية" إلى نظرية التذبذبات الكهربائية. يمكن تفسير المعنى المادي للكثافة الطيفية على النحو التالي.

لنفترض أن الجهد المطبق على مقاومة أومية قدرها 1 أوم، فإن متوسط ​​القدرة المتبددة عبر هذه المقاومة بمرور الوقت يساوي

إذا قمنا بزيادة فترة المراقبة إلى حدود لا نهائية واستخدمنا (9.30)، (9.38)، (9.55)، فيمكننا كتابة صيغة متوسط ​​القدرة على النحو التالي:

توضح المساواة (9.57) أنه يمكن تمثيل متوسط ​​قوة الإشارة كمجموع لا نهائي من المصطلحات متناهية الصغر، والتي تمتد إلى جميع الترددات من 0 إلى

يلعب كل حد أولي من هذا المجموع دور القدرة المقابلة لجزء متناهي الصغر من الطيف الموجود في النطاق من إلى. كل قوة أولية تتناسب مع قيمة الوظيفة لتردد معين الكثافة هي أنها تميز توزيع طاقة الإشارة عبر طيف التردد.

يمكن إيجاد الكثافة الطيفية تجريبياً من خلال القيمة المتوسطة للسعة التربيعية لتوافقيات تنفيذ عملية عشوائية. الأدوات المستخدمة لهذا الغرض والتي تتكون من محلل الطيف وآلة حاسبة لمتوسط ​​قيمة السعة التوافقية التربيعية تسمى مقاييس الطيف. إن العثور على الكثافة الطيفية تجريبياً أكثر صعوبة من إيجاد دالة الارتباط، لذلك عملياً، يتم حساب الكثافة الطيفية في أغلب الأحيان باستخدام دالة ارتباط معروفة باستخدام الصيغة (9.52) أو (9.53).

يتم تعريف الكثافة الطيفية المتبادلة لعمليتين عشوائيتين ثابتتين على أنها تحويل فورييه لوظيفة الارتباط المتبادل، أي.

وباستخدام الكثافة الطيفية المتبادلة، وبتطبيق تحويل فورييه العكسي إلى (9.58)، يمكننا إيجاد تعبير لدالة الارتباط المتبادل:

الكثافة الطيفية المتقاطعة هي مقياس للعلاقة الإحصائية بين عمليتين عشوائيتين ثابتتين: إذا كانت العمليات غير مترابطة ولها قيم متوسطة صفر، فإن الكثافة الطيفية المتقاطعة تكون صفرًا، أي.

على عكس الكثافة الطيفية، فإن الكثافة الطيفية المتقاطعة ليست دالة زوجية لـ o وليست دالة حقيقية، ولكنها دالة معقدة.

دعونا نفكر في بعض خصائص الكثافات الطيفية

1 تكون الكثافة الطيفية لعملية عشوائية خالصة، أو الضوضاء البيضاء، ثابتة عبر مدى التردد بأكمله (انظر الشكل 5.9، د):

في الواقع، استبدال التعبير (9.47) لوظيفة ارتباط الضوضاء البيضاء إلى (9.52)، نحصل عليه

إن ثبات الكثافة الطيفية للضوضاء البيضاء على كامل نطاق التردد اللانهائي، الذي تم الحصول عليه في التعبير الأخير، يعني أن طاقة الضوضاء البيضاء يتم توزيعها بالتساوي عبر الطيف بأكمله، وأن الطاقة الإجمالية للعملية تساوي اللانهاية. ويشير هذا إلى الاستحالة المادية لعملية عشوائية مثل الضوضاء البيضاء. الضوضاء البيضاء هي تجسيد رياضي لعملية حقيقية. في الواقع، يسقط طيف التردد عند ترددات عالية جدًا (كما هو موضح بالخط المنقط في الشكل 9.5، د). ومع ذلك، إذا كانت هذه الترددات عالية جدًا بحيث لا تلعب دورًا عند النظر في أي جهاز معين (لأنها تقع خارج نطاق التردد المرسل بواسطة هذا الجهاز)، فإن تحسين الإشارة في شكل ضوضاء بيضاء يبسط الاعتبار ويسهل وبالتالي مناسبة تماما.

يتم تفسير أصل مصطلح "الضوضاء البيضاء" من خلال تشبيه مثل هذه العملية بالضوء الأبيض، الذي له نفس شدة جميع المكونات، وحقيقة أن العمليات العشوائية مثل الضوضاء البيضاء تم تحديدها لأول مرة في دراسة الحرارة تذبذب الضوضاء في أجهزة الهندسة الراديوية.

2. الكثافة الطيفية للإشارة الثابتة هي دالة تقع عند أصل الإحداثيات (انظر الشكل 9.5، أ)، أي.

ولإثبات ذلك، لنفترض أن الكثافة الطيفية لها الشكل (9.62)، ومن (9.55) دالة الارتباط المقابلة. لأن

ثم عندما نحصل

وهذا (وفقًا للخاصية 5 من وظائف الارتباط) يعني أن الإشارة المقابلة للكثافة الطيفية المحددة بواسطة (9.62) هي إشارة ثابتة تساوي

حقيقة أن الكثافة الطيفية هي دالة تعني أن كل قدرة إشارة التيار المستمر تتركز عند تردد صفر، كما هو متوقع.

3. تمثل الكثافة الطيفية للإشارة الدورية وظيفتين تقعان بشكل متناظر بالنسبة لأصل الإحداثيات عند (انظر الشكل 9.5، هـ)، أي.

ولإثبات ذلك لنفترض أن الكثافة الطيفية لها الشكل (9.63)، وباستخدام (9.55) نجد دالة الارتباط المقابلة:

وهذا (وفقاً لخاصية 6 دوال ارتباط) يعني أن الإشارة المقابلة للكثافة الطيفية المحددة بـ (9.63) هي إشارة دورية تساوي

وحقيقة أن الكثافة الطيفية تمثل وظيفتين تقعان في يعني أن كل قوة الإشارة الدورية تتركز في ترددين: فإذا أخذنا الكثافة الطيفية في منطقة الترددات الموجبة فقط، نحصل على،

أن كل قوة الإشارة الدورية سوف تتركز على تردد واحد.

4. بناءً على ما سبق، فإن الكثافة الطيفية للدالة الزمنية الموسعة في سلسلة فورييه لها الشكل

تتوافق هذه الكثافة الطيفية مع طيف خطي (الشكل 9.9) مع وظائف تقع عند ترددات توافقية إيجابية وسلبية. في التين. 9.9 - يتم تصوير الوظائف بشكل تقليدي بحيث تظهر ارتفاعاتها بما يتناسب مع معاملات الوحدة - الوظيفة، أي القيم و

لاحظ أن الكثافة الطيفية، كما يلي من (9.64)، لا تحتوي، مثل دالة الارتباط المحددة بواسطة (9.44)، على أي معلومات حول التحولات الطورية للمكونات التوافقية الفردية. والعكس صحيح. وهذا يتوافق مع الجوهر المادي للعملية: كلما اتسع الرسم البياني للكثافة الطيفية، أي كلما تم تمثيل الترددات الأعلى في الكثافة الطيفية، زادت درجة تباين العملية العشوائية ونفس الرسوم البيانية لوظيفة الارتباط. بمعنى آخر، العلاقة بين نوع الكثافة الطيفية ونوع دالة الزمن هي علاقة عكسية مقارنة بالعلاقة بين دالة الارتباط ونوع دالة الزمن. هذا صحيح بشكل خاص عند النظر في إشارة ثابتة والضوضاء البيضاء. في الحالة الأولى، تكون دالة الارتباط على شكل خط مستقيم أفقي، وتكون الكثافة الطيفية على شكل -function (انظر الشكل 9.5، أ). وفي الحالة الثانية (انظر الشكل 9.5، د) تحدث الصورة المعاكسة.

6. تحتوي الكثافة الطيفية للعملية العشوائية، التي تتراكب عليها المكونات الدورية، على جزء متصل ووظائف منفصلة تتوافق مع ترددات المكونات الدورية.

تشير القمم الفردية في مخطط الكثافة الطيفية إلى أن العملية العشوائية مختلطة بمكونات دورية مخفية قد لا يتم اكتشافها للوهلة الأولى في السجلات الفردية للعملية. على سبيل المثال، إذا تم فرض إشارة دورية واحدة ذات تردد على عملية عشوائية، فإن الرسم البياني؛ الكثافة الطيفية لها الشكل الموضح في الشكل. 9.10,

في بعض الأحيان يتم تقديم معيار طبيعي في الاعتبار

الكثافة الطيفية وهي صورة فورييه لدالة الارتباط الطبيعية (9.48):

الكثافة الطيفية الطبيعية لها البعد الزمني.

المحاضرة 7.

كثافة الطاقة الطيفية لعملية عشوائية

عندما نعني عملية عشوائية كمجموعة (مجموعة) من الإنجازات، فمن الضروري أن نأخذ في الاعتبار أن الإنجازات ذات الأشكال المختلفة تتوافق مع خصائص طيفية مختلفة. يؤدي حساب متوسط ​​الكثافة الطيفية المعقدة على جميع التطبيقات إلى طيف صفر للعملية (بمتوسط ​​= 0) بسبب العشوائية واستقلالية أطوار المكونات الطيفية في التطبيقات المختلفة. ومع ذلك، من الممكن تقديم مفهوم الكثافة الطيفية لمتوسط ​​المربع لمتغير عشوائي، حيث أن قيمة المربع المتوسط ​​لا تعتمد على العلاقة الطورية للتوافقيات المجمعة. إذا كانت الدالة العشوائية x(t) تعني الجهد الكهربائي أو التيار، فيمكن اعتبار المربع المتوسط ​​لهذه الدالة بمثابة متوسط ​​الطاقة المتحررة في مقاومة 1 أوم. ويتم توزيع هذه القوة على ترددات في نطاق معين، حسب آلية تكوين العملية العشوائية. متوسط ​​الكثافة الطيفية للطاقة هو متوسط ​​القدرة لكل هرتز عند تردد معين ω . الكثافة الطيفية المقدمة بهذه الطريقة س(ω) في ما يلي سوف نسمي طيف الطاقة للوظيفة س(ر) . يتم تحديد معنى هذا الاسم حسب أبعاد الوظيفة س(ω) ، وهي نسبة القدرة إلى نطاق التردد:

[س(ω) ] = [ الطاقة/عرض النطاق الترددي ] = [الطاقة×الوقت] = [الطاقة]،

ويمكن العثور على طيف الطاقة إذا عرفت آلية تكوين العملية العشوائية. وهنا سنقتصر على بعض التعريفات العامة.

طرق حساب PSD

يمكن تعريف دوال الكثافة الطيفية بثلاث طرق متكافئة مختلفة، والتي سننظر إليها أدناه:

استخدام وظائف التغاير.

استخدام تحويل فورييه المحدود؛

استخدام التصفية والتربيع والمتوسط.

تحديد الأطياف باستخدام وظائف الارتباط.

تاريخيًا، ظهرت أول طريقة لتحديد الكثافة الطيفية في الرياضيات. وهو يتألف من أخذ تحويل فورييه لدالة الارتباط المحسوبة مسبقًا. بعد طرح الوسائل، عادة ما تكون تحويلات فورييه (اللانهائية) موجودة حتى لو كان تحويل فورييه (اللانهائي) للعملية الأصلية غير موجود. ويعطي هذا النهج كثافة طيفية ثنائية الاتجاه محددة للترددات Fمن - إلى + ويشار إليه س(F) .

يجب أن تكون هناك وظائف الارتباط والارتباط المتبادل ر س(ر), راي(ر) و آركسي(ر) . ولنفترض أيضًا أن تكاملات قيمها المطلقة محدودة

ر( د

ومن الناحية العملية، يتم دائمًا تلبية هذه الشروط للتطبيقات ذات الطول المحدود. ثم وظائف PF ر(ر) موجودة ويتم تحديدها بواسطة الصيغ

س س (و)=

س ص (و)= (1)

Sxy (و)=

مثل هذه التكاملات على الإنجازات المحدودة موجودة دائمًا. المهام سكس(F) و س ص(F) تسمى وظائف الكثافة الطيفية للعمليات س(ر) و ذ(ر) على التوالي، أو ببساطة الكثافة الطيفية، والوظيفة تسمى الكثافة الطيفية المتبادلة للعمليتين س(ر) و ذ(ر) .

معكوس PFs من الصيغ (1) يعطي

ر س(τ ) =

راي(τ ) = (2)

آركسي(τ ) = df.

تسمى العلاقات (1) و (2) بصيغ Wiener-Khinchin، والتي أنشأت بشكل مستقل في الثلاثينيات علاقة بين وظائف الارتباط والكثافة الطيفية من خلال PF. عند حل المشكلات العملية، يجب على المرء أن يسمح بذلك ر(ر) و س(F) وجود وظائف دلتا.

من خصائص التماثل لوظائف التغاير الثابتة يتبع

س س (-و)= س س (و)أ S xy (-f) = S yx (f)

وبالتالي الكثافة الطيفية سكس(F) هي دالة زوجية حقيقية، أ س س ص(F) - وظيفة معقدة من F.

ثم يمكن تحويل العلاقات الطيفية من (1) إلى النموذج

عندما نعني عملية عشوائية كمجموعة (مجموعة) من وظائف الزمن، فمن الضروري أن نأخذ في الاعتبار أن الوظائف ذات الأشكال المختلفة تتوافق مع خصائص طيفية مختلفة. يؤدي حساب متوسط ​​الكثافة الطيفية المعقدة المقدمة في الفقرة 2.6 أو 2.1 على جميع الوظائف إلى طيف صفري للعملية (في ) بسبب عشوائية واستقلالية أطوار المكونات الطيفية في التطبيقات المختلفة.

ومع ذلك، من الممكن تقديم مفهوم الكثافة الطيفية لمتوسط ​​مربع دالة عشوائية، حيث أن قيمة متوسط ​​المربع لا تعتمد على العلاقة الطورية للتوافقيات المجمعة. إذا كانت الدالة العشوائية تعني جهدًا كهربائيًا أو تيارًا كهربائيًا، فيمكن اعتبار متوسط ​​مربع هذه الدالة متوسط ​​الطاقة المتحررة في مقاومة قدرها 1 أوم. ويتم توزيع هذه القوة على ترددات في نطاق معين، حسب آلية تكوين العملية العشوائية. متوسط ​​الكثافة الطيفية للطاقة هو متوسط ​​القدرة لكل هرتز عند تردد معين. البعد الخاص بالوظيفة، وهو نسبة القدرة إلى نطاق التردد، هو

ويمكن معرفة الكثافة الطيفية للعملية العشوائية إذا كانت آلية تكوين العملية العشوائية معروفة. وفيما يتعلق بالضوضاء المرتبطة بالبنية الذرية للمادة والكهرباء، سيتم تناول هذه المشكلة في الفقرة 3.7. هنا سنقتصر على بعض التعريفات العامة.

من خلال اختيار أي تحقيق من المجموعة وتحديد مدته بفاصل زمني محدود T، يمكنك تطبيق تحويل فورييه المعتاد عليه والعثور على الكثافة الطيفية (ω). ثم يمكن حساب طاقة الجزء المدروس من التنفيذ باستخدام الصيغة (2.66):

بتقسيم هذه الطاقة نحصل على متوسط ​​قوة التنفيذ k على الجزء T

ومع زيادة T، تزداد الطاقة، ولكن النسبة تميل إلى حد معين. بعد أن تجاوزنا الحد الذي حصلنا عليه

يمثل متوسط ​​الكثافة الطيفية لقدرة التنفيذ المعني.

بشكل عام، يجب أن يتم حساب متوسط ​​القيمة على العديد من التطبيقات. في هذه الحالة، وقصر أنفسنا على النظر في عملية ثابتة وعملية، يمكننا أن نفترض أن الوظيفة التي تم العثور عليها من خلال حساب المتوسط ​​على تطبيق واحد تميز العملية برمتها ككل.

بحذف المؤشر k، نحصل على التعبير النهائي لمتوسط ​​قوة العملية العشوائية

إذا تم أخذ عملية عشوائية ذات قيمة متوسطة غير الصفر في الاعتبار، فيجب تمثيل الكثافة الطيفية في النموذج